回溯解法

前言

回溯问题的本质实际上还是树的遍历。

回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度，下面的图来自代码随想录：

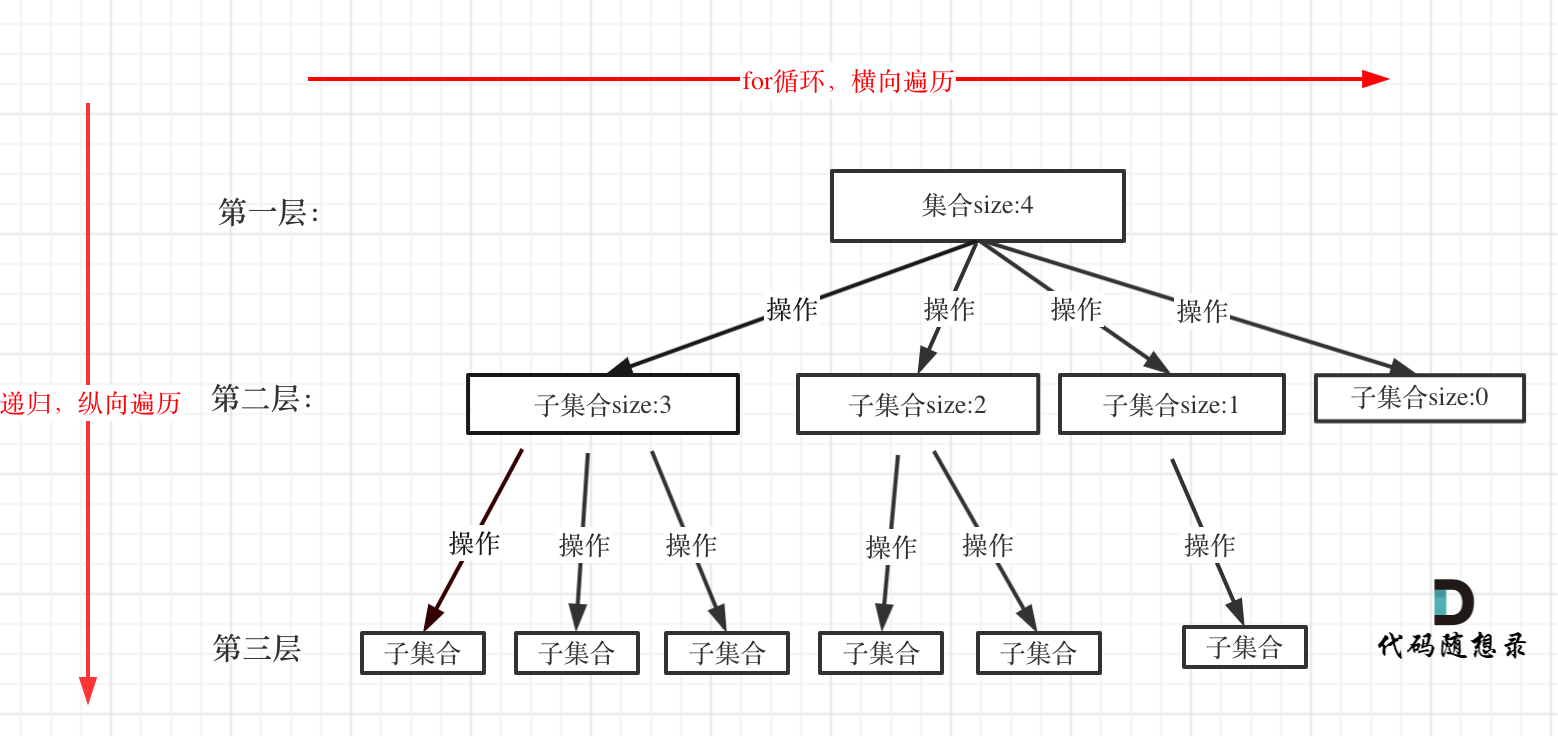那如何回溯呢？就比如说，图中的递归问题遍历到了第三层第一个元素，我们知道在第一层和第二层已经选择过的决策中，还有其他决策（兄弟节点）可以选择，那么就将第三层已经遍历后的状态恢复到遍历之前，但是要给第三层第一个节点加上已遍历的标签，让它继续去第三层搜索其他可能的结果，这就是“回溯”的意义。

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

Leetcode46 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

思路

画出思路，以[1,2,3]为例

在画图图解之后，可以发现，在递归的过程中，需要标记出nums数组哪些数已经被加入到了path中，所以这个时候需要维持一个布尔数组，来表示nums数据被使用的标记，下面是代码：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
		result = []
		def backTrack(path: List[int], used: List[bool]):
			# 边界条件：选够数字了
			if len(path) == len(nums):
				result.append(path[:])
				return
			for index in range(len(nums)):
				# 如果这个数已经被标记了，就直接跳过
				if used[index]:
					continue
				path.append(nums[index])
				used[index] = True
				
				backTrack(path,used)

				# 回溯
				
				path.pop()
				used[index] = False
		backTrack([],[False] * len(nums))
		return result