长度最小的子数组题解

winkz

2024-07-01

题目

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

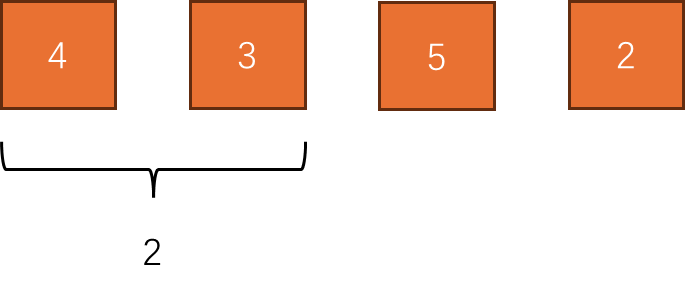
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

题解

首先这里可以用暴力想到，直接遍历每个子数组，求和，然后取每趟最小的那个序列。这里有一个小tips：在每个求和的子序列中，一旦找到第一个符合要求的长度，那么这轮最小长度必然是该长度，这时直接跳出循环，进行下一轮循环就可以了，代码也很简单。

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        length = len(nums)
		# 这里的minLen初始值给它设置为无穷大
        minLen = float('inf')
		for i in range(length):
			sums = 0
			for j in range(i,length):
				sums += nums[j]
				if sums >= target:
					minLen = min(minLen,i-j +1)
					break
        return 0 if minLen == float('inf') else minLen

这种写法双循环，时间复杂度O(n^2)，空间复杂度O(1)

为了优化这种方法，考虑是否可以一轮遍历就完成最小值的筛选？答案是可以的，使用滑动窗口策略可以达到这个目的。

这里我的想法是：既然要在一次循环内完成最小子数组长度的筛选，不仅需要一个指针在前面“拉”，还需要在每次计算完sum值之后，在后面“推”，把区间“挤”到其可能的最小值，图来自代码随想录：

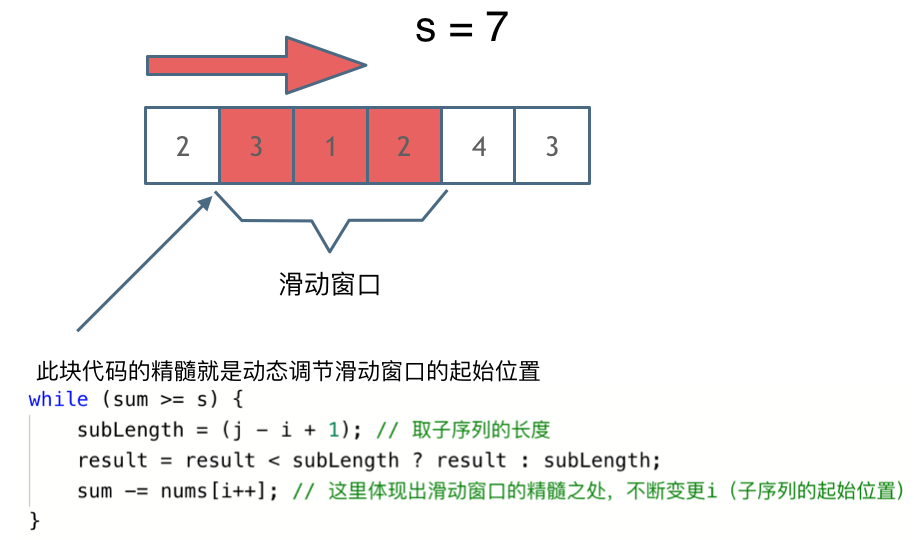
根据这个思路，代码如下所示：

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        length = len(nums)
        minLen, sums, i = float('inf'), 0, 0
        for j in range(length):
            sums += nums[j]
            while target <= sums:
                minLen = min(minLen, j - i + 1)
                sums -= nums[i]
                i += 1
        return 0 if minLen == float('inf') else minLen

在每次循环计算过后，i指针都会往前“挤”，直到挤到小于targe的大小，然后j指针再向前“寻找机会”。

该算法一次遍历，时间复杂度为O(n)，空间复杂度为常量。